Análisis de agrupación y jerarquía de los pendientes celtiformes antropomórficos de la Colección de Dumbarton Oaks

 

David F. Mora-Marín
davidmm@unc.edu
University of North Carolina
Chapel Hill

26/12/2022

 

Este blog presenta un ejemplo de cómo utilizar métodos cuantitativos para el estudio de los pendientes de jade chibchenses de Costa Rica. Utilizaré los ejemplos de pendientes celtiformes antropomórficos que estudié en Mora-Marín (2021a, 2021b), que forman parte de la Colección de Dumbarton Oaks. Para el análisis emplearé el calculador de estadísticas DATAtab (DATAtab Team 2022).

 

El Cuadro 1 provee los datos básicos de los 17 pendientes estudiados, mientras que el Cuadro 2 provee las estadísticas descriptivas.

 

Cuadro 1. Datos básicos de los 17 pendientes.

Artefacto	Lámina	Longitud	Hoja/Filo	Ancho	Espesor	Peso	Proporción de Hoja/Filo
PC.B.215	21	21.7	9.11	6.67	2.22	500.92	42%
PC.B.216	22	17.3	8.13	5.24	1.76	269.82	47%
PC.B.217	19	12.38	5.26	5.08	1.91	225.41	42.5%
PC.B.219	50	14.29	6.6	1.59	1.27	58.6	46%
PC.B.221	42	13.02	5.6	1.91	0.95	37.25	42.7%
PC.B.222	53	11.43	5.37	2.54	1.59	51.94	47%
PC.B.223	20	9.53	4.0	4.76	1.27	108.99	42%
PC.B.224	18	8.57	4.1	3.81	1.27	67.27	47.6%
PC.B.226	16	8.26	3.63	4.13	1.27	71.43	44%
PC.B.227	23	7.3	2.8	3.49	0.95	31.55	36.6%
PC.B.235	24	5.72	2.21	3.18	0.64	18.38	38.7%
PC.B.262	43	8.26	3.4	2.22	0.74	22.43	41%
PC.B.251	25	5.72	2.0	4.13	1.27	72.4	35%
PC.B.289	17	6.99	2.7	3.3	0.95	35.65	38%
PC.B.290	5	9.31	3.63	4.45	1.35	89.34	39%
PC.B.292	44	10.16	5.5	2.54	1.32	48.11	54%

 

Cuadro 2. Estadísticas descriptivas.

	Longitud	Hoja/Filo	Ancho	Espesor	Peso	Proporción de Hoja/Filo
Mean	10.62	4.63	3.69	1.3	106.84	42.69
Median	9.42	4.05	3.65	1.27	62.94	42.25
Modal	5.72	3.63	2.54	1.27	18.38	42
Std. Deviation	4.33	2.05	1.37	0.42	126.37	4.85
Minimum	5.72	2	1.59	0.64	18.38	35
Maximum	21.7	9.11	6.67	2.22	500.92	54
Number of valid values	16	16	16	16	16	16

 

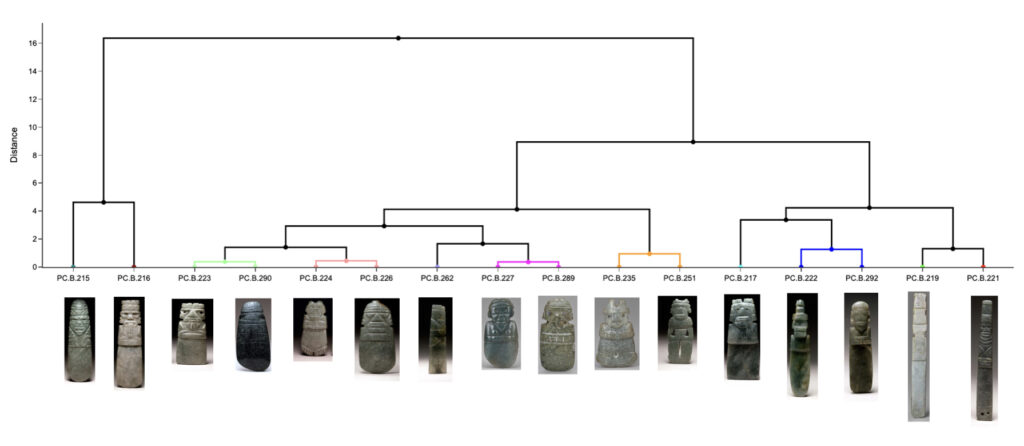
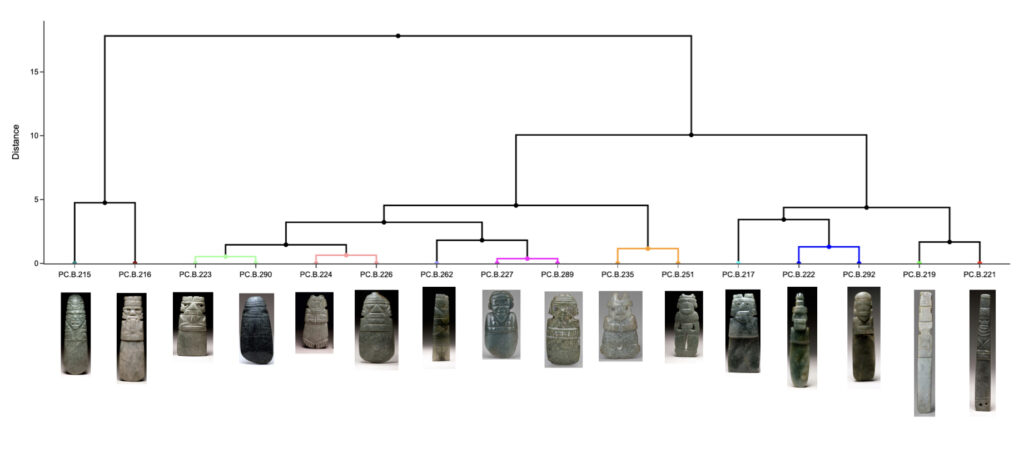
La primera pregunta que quise investigar es la de posibles agrupaciones en base a las dimensiones físicas de los pendientes. Para ello utilicé el calculador de agrupaciones jerárquicas de DATAtab, específicamente mediante el método de enlace completo y de distancia euclidiana. La Figura 1 muestra el resultado en base a dos dimensiones: longitud y ancho. La Figura 2 muestra el resultado de añadir el espesor y la longitud de la hoja/filo del pendiente. La gran similitud entre los modelos de las Figuras 1 y 2 sugieren que longitud y ancho bien podrían ser suficientes para establecer agrupaciones de utilidad. Estas agrupaciones podrían ser el resultado de una variedad de causas: subregionalismos, distintas tradiciones de artesanos a través del tiempo, distintas materias primas, distintos temas artísticos, etc. Por supuesto, dado el hecho de que estos artefactos carecen de procedencia, no es posible investigar ninguna de las primeras dos posibilidades.

 

Figura 1. Dendograma de agrupaciones por longitud y ancho. (Las imágenes de los pendientes no están mostradas a escala.)

Figura 2. Dendograma de agrupaciones por longitud, ancho, espesor y longitud de hoja/filo. (Las imágenes de los pendientes no están mostradas a escala.)

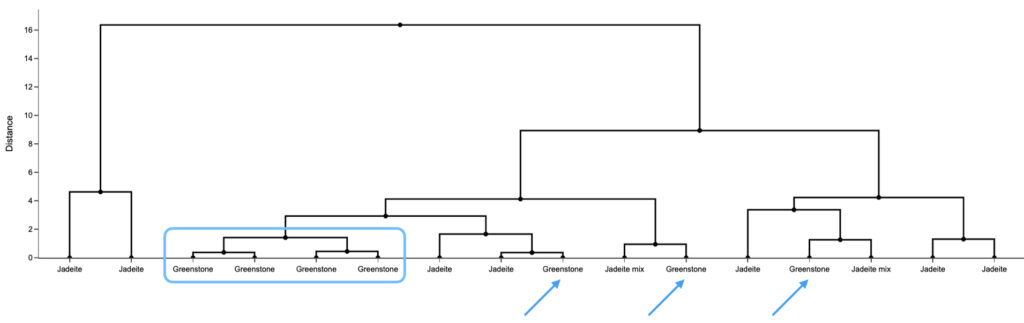
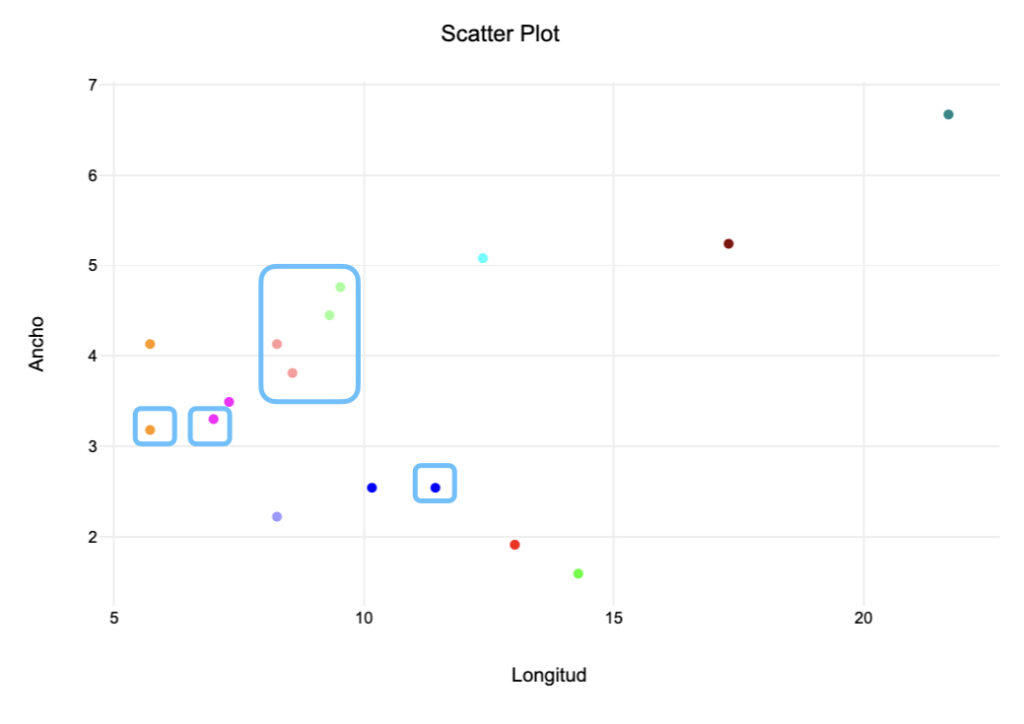
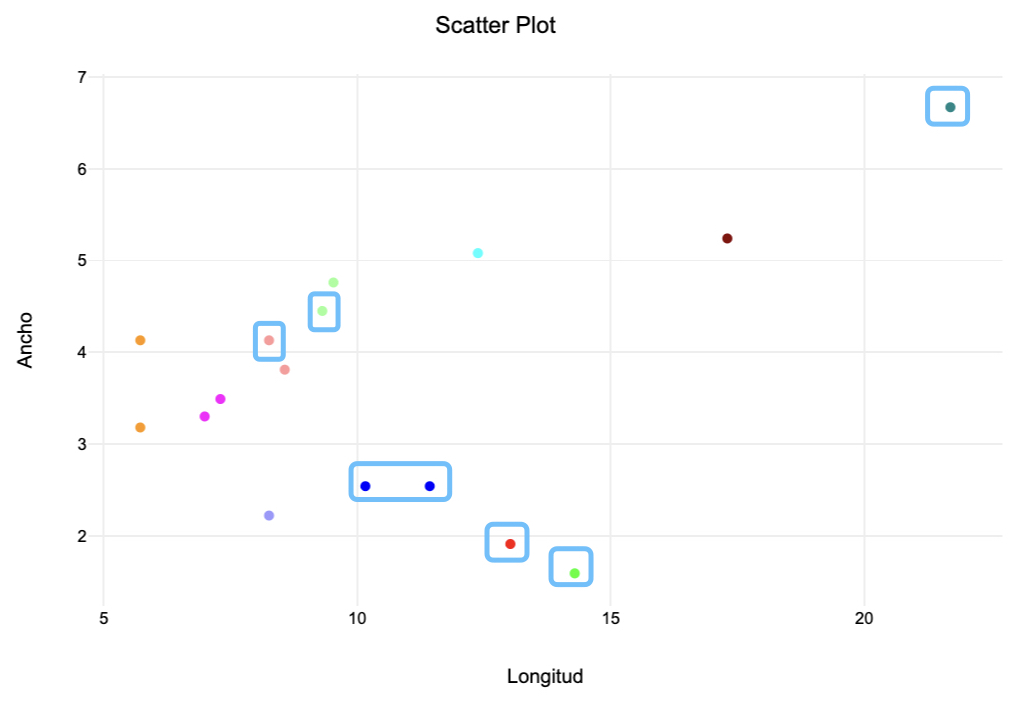
Se puede utilizar el dendograma de la Figura 1 para hacer una inspección visual de las agrupaciones con respecto a la variable de composición. Se dividieron los pendientes en tres grupos: jadeíta (jadeite), combinación de jadeíta (con otros minerales) (jadeite mix) y piedra verde (greenstone). Como se puede ver en la Figura 3, cuatro de los 7 ejemplos compuestos de piedra verde forman una agrupación algo estrecha. La Figura 4 muestra el diagrama de dispersión correspondiente a la misma información utilizada para el análisis de agrupación jerárquica; los ejemplos de piedra verde se muestran dentro de rectángulos.  Tal distribución podría sugerir una relación entre las dimensiones de longitud y ancho, por un lado, y la composición del pendiente, por el otro.

 

Figura 3.

 

Figura 4. Diagrama de dispersión con ejemplos de piedra verde dentro de rectángulos.

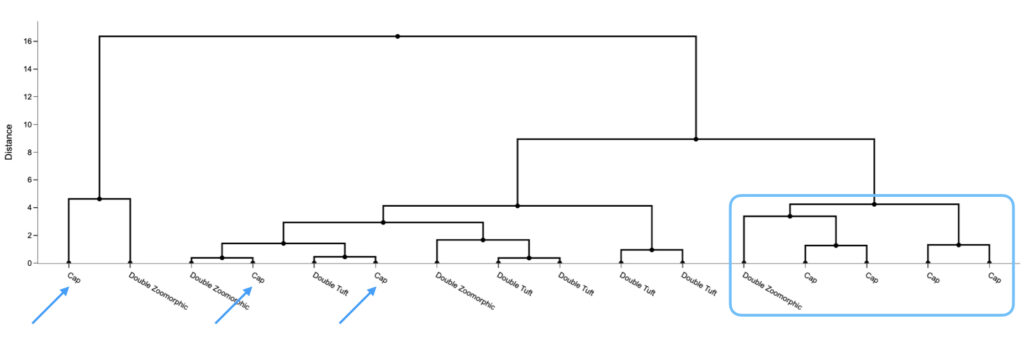
También, el dendograma de agrupaciones, visto desde el punto de vista de los motivos de los tocados (gorro = cap, doble penacho = double tuft, doble zoomórfico = double zoomorphic), como en la Figura 6, pareciera mostrar una agrupación densa del motivo de gorro, especialmente con respecto a la longitud de los pendientes, con cuatro de los siete ejemplos mostrando valores similares, como se aprecia en la Figura 7.

 

Figura 5.

 

Figura 6. Diagrama de dispersión con ejemplos de motivos de gorro dentro de rectángulos

 

Para determinar si estos patrones aparentes tiene alguna significancia estadística, se realizaron varias pruebas. Las pruebas de Kruskal-Wallis realizadas no mostraron significancia estadística, con valores p por encima del valor mínimo de .05. Sin embargo, un análisis de regresión logística con la composición como variable dependiente y la longitud y ancho como variables independientes sugiere algo distinto: el modelo (Cuadro 3) muestra que un incremento en longitud se asocia con un incremento en la probabilidad de que el pendiente sea de jadeíta, y que tal asociación posee significancia estadística (valor p = .045). Aunque el análisis mostró una correlación negativa entre los pendientes de “piedra verde” y la longitud, tal asociación no muestra significancia estadística (valor p = .065). El ancho de los pendientes no mostró ninguna relación con la variable de composición.

 

Cuadro 3. Regresión logística para variante Jadeite (variable Composition)

a. Resultado para predicción de variante Jadeite (variable Composition)

Total number of cases	Correct assignments	In percent
16	12	75%

b. Cuadro de clasificación

		Predicted
		not Jadeite	Jadeite	Correct
Observed	not Jadeite	7	2	77.78%
	Jadeite	2	5	71.43%
	Total			75%

c. Chi2

Chi2	df	p
7.67	2	0.022

d. Resumen del modelo para variante Jadeite (variable Composition)

-2 Log-Likelihood	Cox & Snell R2	Nagelkerke R2	McFadden’s R2
14.26	0.38	0.51	0.35

e. Modelo para variante Jadeite (variable Composition)

	Coefficient B	Standard error	z	p	Odds Ratio	95% conf. interval
Length	0.5	0.25	1.97	0.049	1.64	1 – 2.7
Width	-0.37	0.59	0.64	0.525	0.69	0.22 – 2.18
Constant	-4.09	3.15	1.3	0.194

 

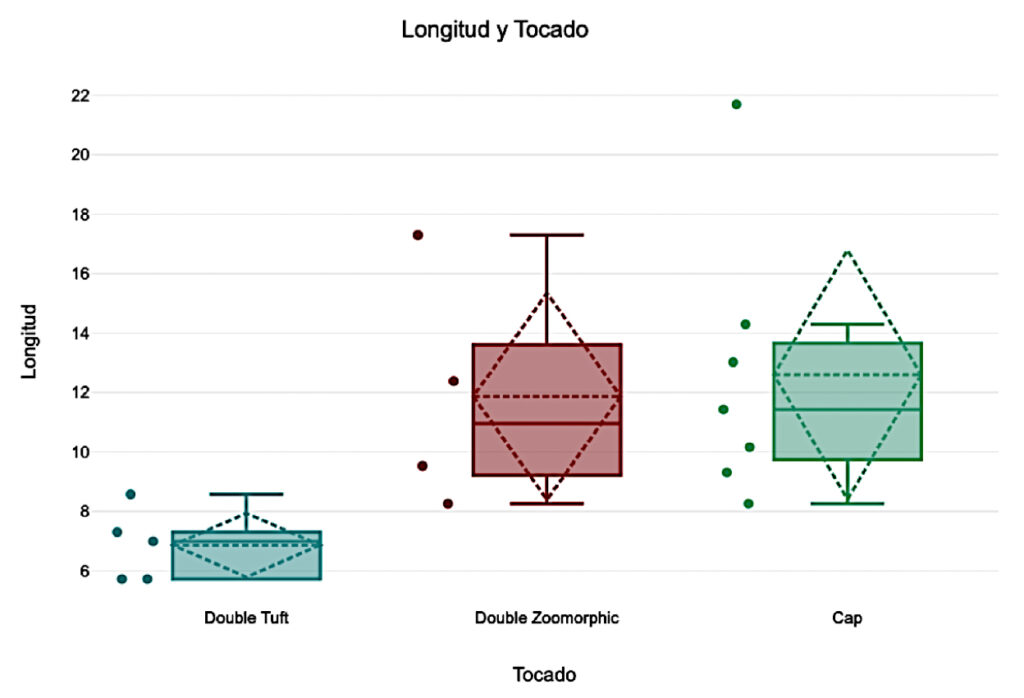
En lo que respecta a los motivos de los tocados, se realizaron también varias pruebas Kruskal-Wallis. La primera analizó si las variantes de la variable Tocado muestran una diferencia significativa con respecto a la longitud. La Figura 7 muestra la distribución de los tres motivos de los tocados con respecto a la longitud de los pendientes. El Cuadro 4 presenta los resultados de esta prueba, los cuales sugieren significancia estadística (valor p = .015), y por ende, que hay una diferencia significativa entre las categorías de la variable Tocado con respecto a la longitud; las pruebas Dunn-Bonferroni señalan que la diferencia significativa es la que distingue al motivo de Doble Penacho (con valores medios más bajos) y Gorro (con valores medios más altos).

 

Figura 7. Distribución de Longitud con respect a tres tipos de Tocado.

 

Cuadro 4. Prueba Kruskal-Wallis para Longitud y variable Tocado.

a. Rangos

Groups	N	Mean Rank
Double Tuft	5	3.4
Double Zoomorphic	4	10.38
Cap	7	11.07
Total	16

b. Estadísticas

	Values
Chi2	8.42
df	2
p	0.015

c. Pruebas Dunn-Bonferroni

	Test Statistic	Std. Error	Std. Test Statistic	p	Adj. p
Double Tuft – Double Zoomorphic	-6.98	3.19	-2.19	0.029	0.086
Double Tuft – Cap	-7.67	2.78	-2.76	0.006	0.018
Double Zoomorphic – Cap	-0.7	2.98	-0.23	0.815	1

 

Ni la anchura ni la proporción de la hoja/filo del pendiente mostraron asociaciones de significancia estadística con la variable Tocado.

 

Para resumir, es posible que los artesanos chibchenses hubiesen preferido: 1) trabajar la jadeíta en formas de pendientes de mayor longitud, a comparación con otras materias primas; y 2) el motivo de Gorro con pendientes de mayor longitud. Pero para concluir, este blog simplemente propone una metodología para investigar los pendientes de jade chibchenses de Costa Rica. No es posible proponer que 17 ejemplos sean representativos de decenas de miles, pero estos mismos métodos se pueden emplear para investigar bases de datos más extensas. Sería importante comenzar con una base de datos de ejemplos con contexto arqueológico, por ejemplo, para intentar de detectar patrones estilísticos, temáticos y composicionales en base a región y período.

 

Referencias

DATAtab Team. (2022). DATAtab: Online Statistics Calculator. DATAtab e.U. Graz, Austria. URL https://datatab.net.

Mora-Marín, David F. 2021a. Artifact Descriptions. En Pre-Columbian Art of Central America and Colombia at Dumbarton Oaks, editado por John Hoopes y Colin McEwan, pp. 80-175. Washington, DC: Dumbarton Oaks Research Library and Collection.

Mora-Marín, David F. 2021b. The Anthropomorphic Celtiform Pendant Theme of the Jade Tradition in Costa Rica. En Pre-Columbian Art of Central America and Colombia at Dumbarton Oaks, editado por John Hoopes y Colin McEwan, pp. 47-60. Washington, DC: Dumbarton Oaks Research Library and Collection.

Hoopes, John, and Colin McEwan, editors. 2021a. Pre-Columbian Art of Central America and Colombia at Dumbarton Oaks. Washington, DC: Dumbarton Oaks Research Library and Collection.

Hoopes, John, and Colin McEwan, editors. 2021b. Pre-Columbian Art of Central America, Colombia, and Ecuador: Toward an Integrated Approach. Washington, DC: Dumbarton Oaks Research Library and Collection.

 

 

Orejas en forma de “c” y el prejuicio fotográfico

David F. Mora-Marín
davidmm@unc.edu
University of North Carolina
Chapel Hill

31/7/2022, 25/12/2022

 

Los lados anversos y reversos de los pendientes celtiformes de “jade” chibchenses de Costa Rica muchas veces son fotografiados desde un ángulo perpendicular a la superficie del artefacto. Esto es indudablemente el resultado de un factor práctico: el hecho de que las publicaciones generalmente permiten un número limitado de imágenes, ya sean dibujos lineales o fotografías, y generalmente los pendientes celtiformes se pueden calificar como relativamente planos, por lo que un par de imágenes mostrando por delante y por detrás captarían la mayoría de la información artística del artefacto. El problema es que tales pendientes no son completamente planos como lo tienden a ser, por ejemplo, las placas de jade mayas. Más bien, los pendientes celtiformes chibchenses suelen mostrar una combinación de grabado plano y tridimensional. Por ello, las fotografías convencionales suelen ignorar rasgos importantes de tales artefactos.

 

Este es un hecho que confronté al tener la oportunidad de examinar los pendientes celtiformes antropomorfos del Dumbarton Oaks Research Library and Collection en enero del 2014, gracias a la invitación por John Hoopes and Colin McEwan para participar en un proyecto de documentación, descripción y análisis del corpus de artefactos de la región de Istmo-Colombia que forman parte de esa Colección (Hoopes y McEwan 2021a, 2021b). En total, examiné 17 pendientes, descritos en detalle en Mora-Marín (2021a), y contextualizados en su marco histórico-cultural más amplio en Mora-Marín (2021b). Dos de los 17 pendientes exhiben orejas en forma de “c,” un rasgo que no se podía apreciar en las fotografías complemente frontales que eran las únicas disponibles en aquel entonces, ya sea en la página web de la Colección o en los archivos impresos de la misma. De hecho, la práctica estándar en colecciones digitales es mostrar solamente el frente: https://collections.lacma.org/node/238041, https://www.metmuseum.org/art/collection/search/313013?ft=costa+rica+jade&offset=40&rpp=40&pos=58, https://www.denverartmuseum.org/en/object/1994.820.

 

Por ejemplo, el pendiente catalogado PC.B.217 (Figura 1A) muestra orejas en forma de “c” cuando se observa desde un ángulo diagonal (Figuras 1B-C).

 

Figura 1

 

Otro ejemplo es el caso de PC.B.292 (Figura 2A), cuya vista lateral, necesaria dada la característica más tridimensional de este pendiente, permite ver la forma “c” de la oreja de la mujer representada en este pendiente (Figura 2B).

 

Figura 2

 

Como ya se observó, hoy en día, la versión digital de la Colección de Dumbarton Oaks sí provee fotografías de tres ángulos distintos para los pendientes celtiformes de jade chibchenses: anverso, reverso y diagonal. La ficha de PC.B.217, con sus fotografías, se puede encontrar en el siguiente enlace: http://museum.doaks.org/objects-1/info/22817. La de PC.B.292 en el siguiente: http://museum.doaks.org/objects-1/info/22819.

 

La moraleja es simple: es necesario publicar fotografías diagonales o laterales para los pendientes del tipo descrito aquí. Algo tan simple como la forma de las orejas de los personajes representados podría ser un rasgo útil para estudiar la variación sincrónica y el cambio diacrónico de los jades chibchenses de Costa Rica. Sin embargo, este rasgo no ha sido documentado sistemáticamente por la práctica convencional de publicar fotografías directamente anversas o reversas.

 

 

Referencias

Mora-Marín, David F. 2021a. Artifact Descriptions. En Pre-Columbian Art of Central America and Colombia at Dumbarton Oaks, editado por John Hoopes y Colin McEwan, pp. 80-175. Washington, DC: Dumbarton Oaks Research Library and Collection.

Mora-Marín, David F. 2021b. The Anthropomorphic Celtiform Pendant Theme of the Jade Tradition in Costa Rica. En Pre-Columbian Art of Central America and Colombia at Dumbarton Oaks, editado por John Hoopes y Colin McEwan, pp. 47-60. Washington, DC: Dumbarton Oaks Research Library and Collection.

Hoopes, John, and Colin McEwan, editors. 2021a. Pre-Columbian Art of Central America and Colombia at Dumbarton Oaks. Washington, DC: Dumbarton Oaks Research Library and Collection.

Hoopes, John, and Colin McEwan, editors. 2021b. Pre-Columbian Art of Central America, Colombia, and Ecuador: Toward an Integrated Approach. Washington, DC: Dumbarton Oaks Research Library and Collection.